The assumptions behind this kernel are that the input operands are
loaded to L1 only one time (i.e., the blocking guarantees that all
of the matrix accessed in the inner loop plus the active panel of
the matrix in the outer loop fits in L1). For very large caches, all
three operands may fit into cache, but this is typically not the
case. Because this gemmK is called by routines that place  as the innermost loop, the output operand
as the innermost loop, the output operand 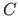 will typically come
from the L2 cache (except, obviously, on the first of the
will typically come
from the L2 cache (except, obviously, on the first of the
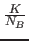 such calls). ATLAS uses the JIK loop variant of
on-chip multiply, and thus all of
such calls). ATLAS uses the JIK loop variant of
on-chip multiply, and thus all of 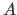 fits in cache, with nu columns
of
fits in cache, with nu columns
of 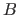 . To take an example, say you are using mu = nu = 4, with
. To take an example, say you are using mu = nu = 4, with
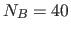 , then the idea is that the
, then the idea is that the 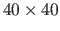 piece of
piece of 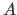 ,
along with the
,
along with the 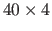 piece of
piece of 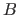 (the active panel of
(the active panel of 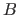 ),
and the
),
and the 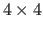 section of
section of 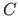 all fit into cache at once, with
enough room for the load of the next step, and any junk the algorithm
might have in L1. That panel of
all fit into cache at once, with
enough room for the load of the next step, and any junk the algorithm
might have in L1. That panel of 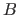 is applied to all of
is applied to all of 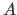 , and then
a new panel is loaded. Since the panel has been applied to all
, and then
a new panel is loaded. Since the panel has been applied to all 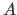 , it
will never be reloaded, and thus we see that
, it
will never be reloaded, and thus we see that 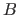 is loaded to L1 only
one time. Since all of
is loaded to L1 only
one time. Since all of 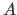 fits in L1, and we keep it there across all
panels of
fits in L1, and we keep it there across all
panels of 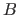 , it is also loaded to L1 only one time.
, it is also loaded to L1 only one time.
If written appropriately, loading all of 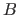 with a few rows
of
with a few rows
of 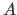 should theoretically be just as efficient (i.e., the IJK variant
of matmul). However, the variants where
should theoretically be just as efficient (i.e., the IJK variant
of matmul). However, the variants where  is not the innermost loop
are unlikely to work well in ATLAS, if for no other reason than the
transpose settings we have chosen militate against it.
is not the innermost loop
are unlikely to work well in ATLAS, if for no other reason than the
transpose settings we have chosen militate against it.
Note that the 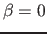 case must not read
case must not read 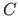 , since the memory may
legally be unitialized.
, since the memory may
legally be unitialized.
Clint Whaley
2012-07-10
![]() with a few rows
of
with a few rows
of ![]() should theoretically be just as efficient (i.e., the IJK variant
of matmul). However, the variants where
should theoretically be just as efficient (i.e., the IJK variant
of matmul). However, the variants where ![]() is not the innermost loop
are unlikely to work well in ATLAS, if for no other reason than the
transpose settings we have chosen militate against it.
is not the innermost loop
are unlikely to work well in ATLAS, if for no other reason than the
transpose settings we have chosen militate against it.
![]() case must not read
case must not read ![]() , since the memory may
legally be unitialized.
, since the memory may
legally be unitialized.