ATLAS 3.5.7 SYRK Timings

So, we've known for a while now that ATLAS's SYRK/HERK perform sub-optimally. It should run roughly at GEMM speed, but it has been instead one of our slowest BLAS. This is bad news, because SYRK is the asymptotic limit to Cholesky performance, just as GEMM is for LU. So, even though Cholesky should run at least as fast as LU, ATLAS's Cholesky has always significantly underperformed.

The solution is to write SYRK in terms of the GEMM kernel, rather than the full GEMM. This has been done for real precision only in 3.5.7, and here are the results.

The first graph compares all DSYRK versions vs DGEMM on a 600Mhz Athlon classic.

DGEMM & DSYRK: ATLAS 3.5.7 vs. 3.5.6 on a 600 Mhz Athlon

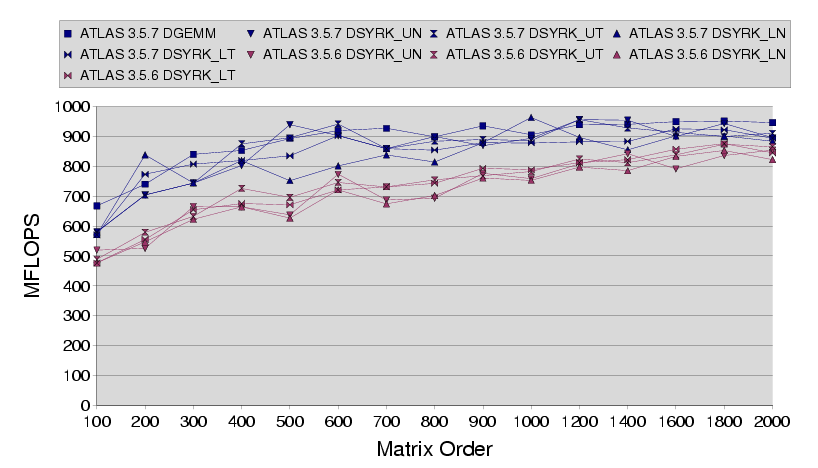
The good news is that SYRK and GEMM speed are now essentially the same, and we see that 3.5.7's SYRK is clearly superior to 3.5.6's. However, the best performing case is 'Upper','NoTrans', which is not used by Cholesky. Since all the cases are relatively close, this is not that big a deal.

Now that our Cholesky performance kernel, DSYRK, is rolling along, what about Cholesky itself:

Factorization results: ATLAS 3.5.7 vs. 3.5.6 on a 600 Mhz Athlon

Again, things are more like what we hoped. Cholesky is still slightly slower than LU for small problems (I believe our LU low-order terms have been better optimized), but catches up around N=600. After this size, Cholesky runs around the same speed as LU, and possibly a little faster.

I include SYRK 'Upper' 'Trans' on this chart, because this is essentially the upper limit on Cholesky performance. Just as with LU, we see that the low-order terms are keeping us from reaching our Cholesky peak.

OK, our final graph is a little busy, but it compares ATLAS 3.5.7 and 3.5.6's differing SYRK, and resulting Cholesky performance on a 1.6 Ghz Opteron.

ATLAS 3.5.7 vs. 3.5.6 on 1 Processor of 1.6Ghz Opteron

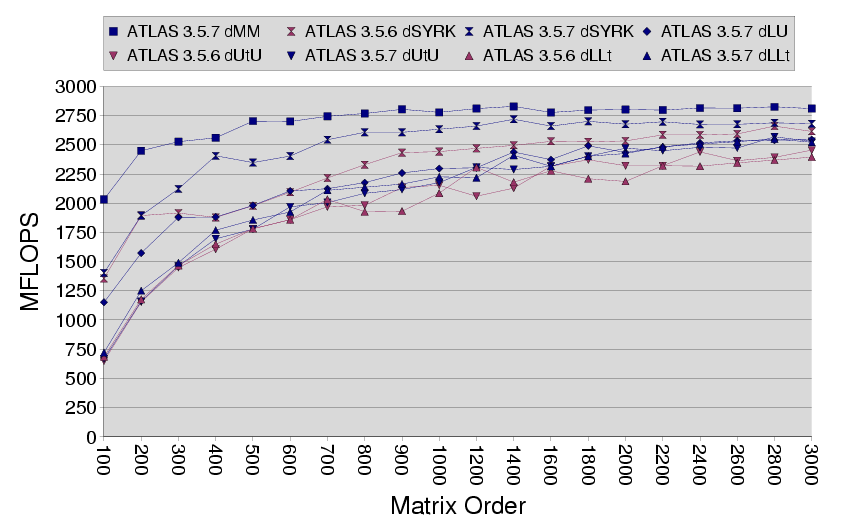
There are several interesting things about this chart. We see that for the small to medium-sized problems, 3.5.7's gemm-kernel-based SYRK kicks butt, but that the recursive gemm-based SYRK used in 3.5.6 catches up asymptotically. 3.5.7's SYRK does not run as fast as GEMM, though actually some cases are closer than this. The case I timed was the one used in Lower Cholesky. If you take the 'Lower' 'Transpose' setting instead, performance will roughly halve the difference between SYRK and GEMM.

3.5.6's Cholesky factorizations never catch up with 3.5.7's, however. It is almost impossible to see on this busy chart, but 3.5.7's Cholesky roughly catches up with LU around N=1000, and they then stay within clock resolution of each other.

Back to ATLAS timing page