ATLAS Itanium 2 Timings

OK, these following graphs are not quite fair to 3.4.2, in that I just took the Itanium 1 defaults for the Itanium 2. With the 128 registers available on the platform, the full search just takes too long to run just to get comparison numbers (3.4 didn't have arch defaults for Itanium 2). Still, the peak performance wouldn't change in any case, and I suspect the Itanium 1 defaults will give reasonable estimates.

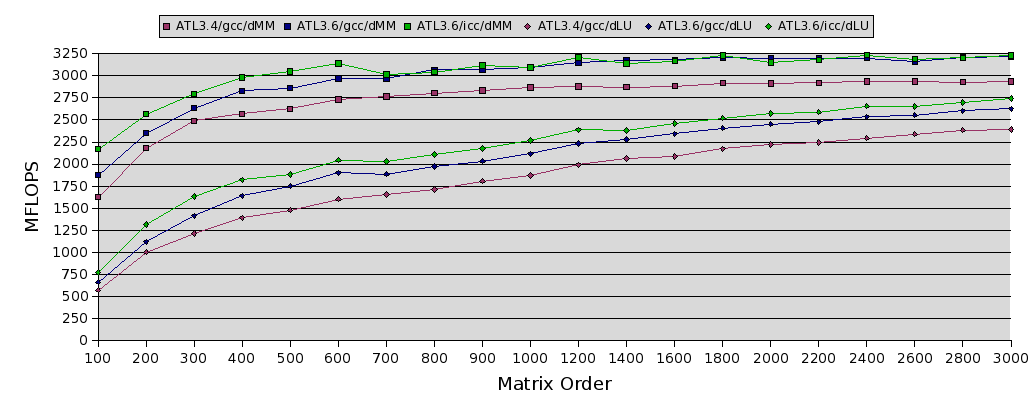
This first graph compares the performance of LU and matrix multiply for three different setups:

  1. ATLAS 3.4.2 using gcc as the compiler
  2. ATLAS 3.6.0 using gcc as the compiler
  3. ATLAS 3.6.0 using icc as the compiler
Support for the Intel compilers is one of the new features of 3.6.0. these compilers provide roughly the same performance as gcc for ATLAS on x86 architectures, but this is not the case on the Itanium 2:

Matrix multiply and LU on 900 Mhz Itanium 2

OK, there are several interesting things on this graph. We see that 3.6.0 is faster than the old release regardless of your compiler. As far as GEMM is concerned, gcc and icc have the same asymptotic performance. This is as expected: they are both using the same kernel, and that kernel is actually compiled by gcc even under ATLAS/icc. Where icc does it's work is in all the cleanup cases, and the other BLAS, where it simply wipes the floor with gcc on taking simple code and using all the IA64's funky architectural features. This translates into a faster LU, even for very large problems where the GEMMs have become indistinguishable.

This next graph is the showstopper. It shows the performance of Cholesky, SYRK and TRSM for the three setups:

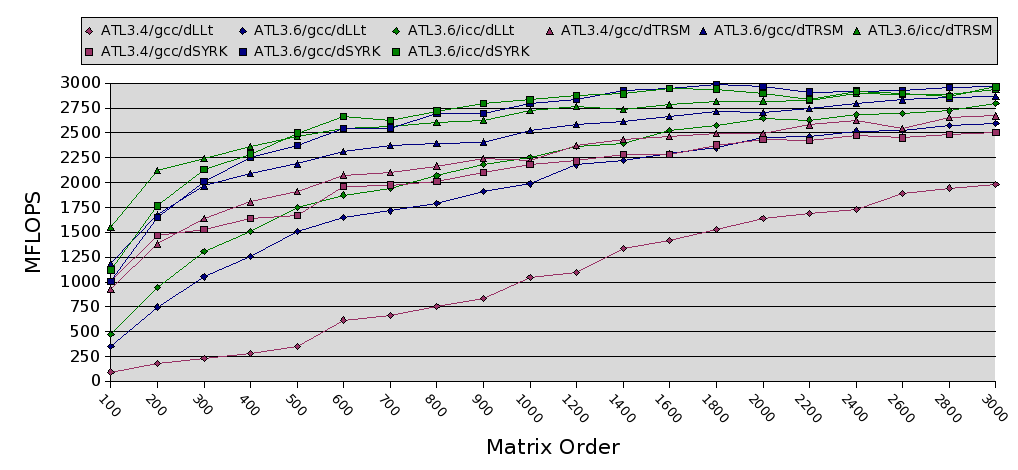
SYRK, TRSM and Cholesky on a 900 Mhz Itanium 2

Now, the first question from this graph is obvious: what the heck happened to 3.4's Cholesky performance? The answer is that there was a performance bug in 3.4's TRSM. It involves when you use a hand-written kernel, and when you use recursion to solve TRSM. Our hand-written kernel is optimized for x86 codes, and does terrible on the IA64, with it's large block size and register set. To fix this problem, you want to use recursion until the problem is quite small. When this fix is applied, the 3.4 code tracks it's TRSM and SYRK performance as 3.6 does (Cholesky's performance is largely driven by these two BLAS).

Back to ATLAS timing page