All routines except SYMV call the GEMV kernel in the same fashion.
Other than SYMV, all routines cannot reduce the load of  from
from  ,
but can reduce the memory access of both
,
but can reduce the memory access of both  and
and  from
from  to
to
 . In general, the
. In general, the  access is reduced by register blocking in
the GEMV kernel. Therefore, the higher level routines block
access is reduced by register blocking in
the GEMV kernel. Therefore, the higher level routines block  such
it is reused across kernel invocations in L1 (if you write a axpy-based
notranspose GEMV kernel,
such
it is reused across kernel invocations in L1 (if you write a axpy-based
notranspose GEMV kernel,  is blocked instead of
is blocked instead of  ). What this amounts
to is partitioning
). What this amounts
to is partitioning  via:
via:
 , where
, where  is the size, in elements,
of the Level 1 cache,
is the size, in elements,
of the Level 1 cache,  is the partitioning of
is the partitioning of  , and
, and  corresponds
to the Yunroll of your input file. The equation is actually a little
more complicated than this, as ATLAS may want to use less than the full
corresponds
to the Yunroll of your input file. The equation is actually a little
more complicated than this, as ATLAS may want to use less than the full
 to avoid cache thrashing and throwing useful sections away between
kernel calls. However, this gives the user some idea of the importance of
these parameters. In particular, it shows that Yunroll should not
be allowed to grow too large, for fear of causing the
to avoid cache thrashing and throwing useful sections away between
kernel calls. However, this gives the user some idea of the importance of
these parameters. In particular, it shows that Yunroll should not
be allowed to grow too large, for fear of causing the  loop to be
too short to support good optimization.
loop to be
too short to support good optimization.
Also, note that after the first invocation of the kernel,  will come
from L1, leaving
will come
from L1, leaving  the dominant data cost.
the dominant data cost.
At present, SYMV does a different blocking that blocks both  and
and
 (all other routines block only one dimension), so that
(all other routines block only one dimension), so that  is reused
between calls to the Transpose and NoTranspose kernels. This may
eventually change as greater sophistication is achieved (as you might
imagine, you get two very different GEMV kernels if one is expecting
is reused
between calls to the Transpose and NoTranspose kernels. This may
eventually change as greater sophistication is achieved (as you might
imagine, you get two very different GEMV kernels if one is expecting
 from main memory, and the other expects
from main memory, and the other expects  to come from L1, as
in this case; this means we may at some time generate a specialized
L1-contained GEMV kernel).
to come from L1, as
in this case; this means we may at some time generate a specialized
L1-contained GEMV kernel).
Note that the 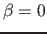 case must not read
case must not read  , since the memory may
legally be unitialized.
, since the memory may
legally be unitialized.
Clint Whaley
2012-07-10
![]() will come
from L1, leaving
will come
from L1, leaving ![]() the dominant data cost.
the dominant data cost.
![]() and
and
![]() (all other routines block only one dimension), so that
(all other routines block only one dimension), so that ![]() is reused
between calls to the Transpose and NoTranspose kernels. This may
eventually change as greater sophistication is achieved (as you might
imagine, you get two very different GEMV kernels if one is expecting
is reused
between calls to the Transpose and NoTranspose kernels. This may
eventually change as greater sophistication is achieved (as you might
imagine, you get two very different GEMV kernels if one is expecting
![]() from main memory, and the other expects
from main memory, and the other expects ![]() to come from L1, as
in this case; this means we may at some time generate a specialized
L1-contained GEMV kernel).
to come from L1, as
in this case; this means we may at some time generate a specialized
L1-contained GEMV kernel).
![]() case must not read
case must not read ![]() , since the memory may
legally be unitialized.
, since the memory may
legally be unitialized.