gemmK usage notes

The assumptions behind this kernel are that the input operands are loaded to L1 only one time (i.e., the blocking guarantees that all of the matrix accessed in the inner loop plus the active panel of the matrix in the outer loop fits in L1). For very large caches, all three operands may fit into cache, but this is typically not the case. Because this gemmK is called by routines that place $K$ as the innermost loop, the output operand $C$ will typically come from the L2 cache (except, obviously, on the first of the $\frac{K}{N_B}$ such calls). ATLAS uses the JIK loop variant of on-chip multiply, and thus all of $A$ fits in cache, with nu columns of $B$. To take an example, say you are using mu = nu = 4, with $N_B = 40$, then the idea is that the $40 \times 40$ piece of $A$, along with the $40 \times 4$ piece of $B$ (the active panel of $B$), and the $4 \times 4$ section of $C$ all fit into cache at once, with enough room for the load of the next step, and any junk the algorithm might have in L1. That panel of $B$ is applied to all of $A$, and then a new panel is loaded. Since the panel has been applied to all $A$, it will never be reloaded, and thus we see that $B$ is loaded to L1 only one time. Since all of $A$ fits in L1, and we keep it there across all panels of $B$, it is also loaded to L1 only one time.

If written appropriately, loading all of $B$ with a few rows of $A$ should theoretically be just as efficient (i.e., the IJK variant of matmul). However, the variants where $K$ is not the innermost loop are unlikely to work well in ATLAS, if for no other reason than the transpose settings we have chosen militate against it.

Note that the 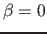$\beta = 0$ case must not read $C$, since the memory may legally be unitialized.